At the turn of the 16th century, Johannes Kepler set out to disprove Copernicus, who believed planets orbited in perfect, concentric circles from the sun. Kepler first formulated his hypothesis: planets had elliptical orbits with two foci, and then set out to prove it mathematically. 4 years and 900 pages of calculations later, he confirmed his theory by determining Mars’s true orbit.
The proof was impressive. But it was remarkable that Kepler managed it — his calculations were riddled with mistakes! Only after repeating his procedures 70 times did he offset his computational errors. With a little less patience, he wouldn’t have proved his theory, and elliptical orbits would have eluded us for longer.
How many Keplers weren't so fortunate?
For most of history, basic calculations were a serious bottleneck to science. A great deal of people, throughout history, have spent a great deal of time coming up with tricks to do it faster. Millennia of their work culminated in the greatest mechanical calculating device there is: the slide rule.
Newton used it to derive the equations of motion, and NASA used it to solve those very equations to take us to the moon. It’s remarkable how little the slide rule has changed in the three centuries spanning these events. But it’s also remarkable how quickly it’s been lost to obscurity in the three decades since.
Multiplying is hard, but adding is easy.
This is the core insight underpinning most number-crunching tricks and, as we'll see, the slide rule.
4,000 years ago, the Babylonians came up with one of the first ways to “hack” multiplication. They realized they could do multiplications once, and write the results on a "cheat-sheet" to avoid having to do them again. But this wasn’t space-efficient — there are 66 ways to multiply two numbers just between 1 and 12 (12 choose 2), so the corresponding cheat-sheet would need 66 pre-computed results. But when your cheat-sheet is more of a cheat-stone-tablet, every result matters.
The next hack came through mathematical identities — "cheat codes" to express one calculation in terms of another. The Babylonians came up with many of these. A classic is the "quarter-square multiplication", which reduces multiplication to subtraction.
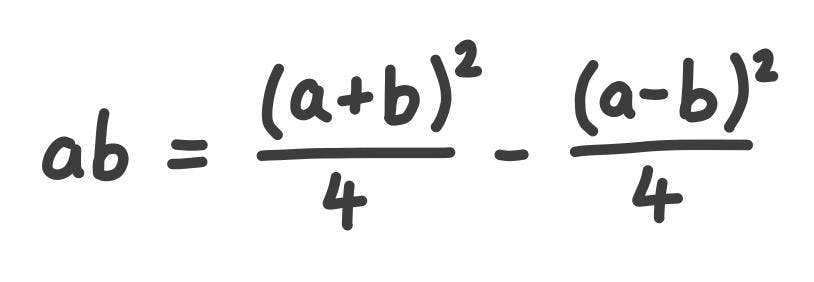
On the face of it, this looks a lot more complicated than just multiplying the damn numbers!
But with the right cheat-sheet, it’s actually simpler: the right-hand-side is always a subtraction of square numbers divided by 4, so by pre-computing these quarter-squares, we can multiply any two numbers by just doing a subtraction. Pre-computing just 24 results now lets us multiply any two numbers between 1 and 12. That’s space efficient!
But this still doesn't scale — to multiply numbers in the 1000s, you’d need to pre-compute thousands of results. We need — somehow — to store fewer results.
Thousands of years later, the solution finally arrived. In 1619, John Napier discovered the ultimate number-crunching cheat-code: the logarithm.
Pierre-Simon Laplace, to whom we owe much of physics and statistics, wrote:
...[the logarithm], by reducing to a few days the labour of many months, doubles the life of the astronomer, and spares him the errors and disgust inseparable from long calculations.
That’s what I’d call a "bicycle for the mind"! How does it work?
We all know that multiplying powers of 10 is easy — we just add the number of zeros:
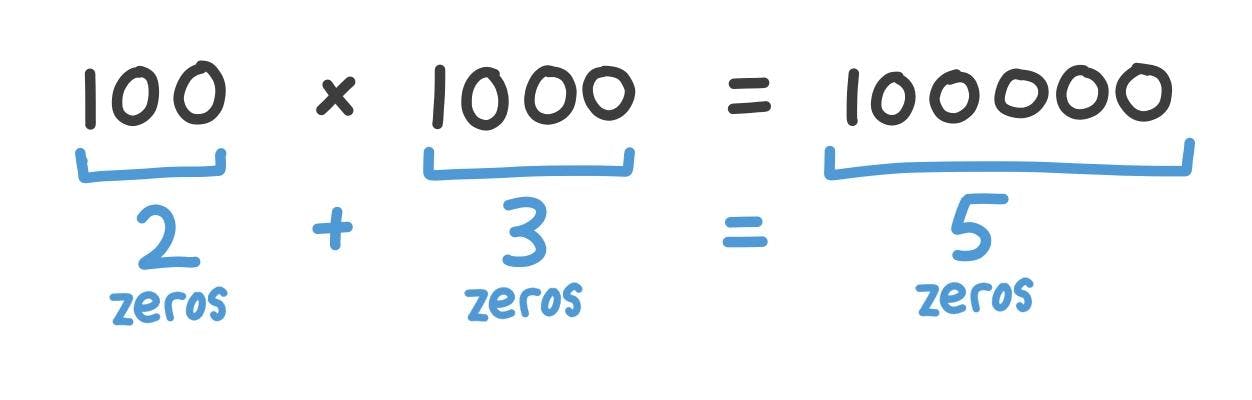
This is actually just a clever application of logarithms! If we can understand how it works, we can generalize it for all numbers.
The "number of zeros" is a special quantity that lets us turn multiplication into addition, but it only works for powers of 10. Is there an equivalent quantity for other numbers?
When we’re counting zeros, what we’re really counting is the number of 10s multiplied together. 100 has two zeros, and comes from multiplying two 10s. So the equivalent for, say, powers of 2, would be the number of 2s multiplied together.
And that’s what the logarithm is — a function that tells you how many times a number was multiplied, by itself, to get another number.
In the world of 10s, the logarithm of x tells you how many times you have to multiply 10 by itself to get that x. In the world of 2s, log(x) tells you how many times you have to multiply 2 by itself to get x.
By converting numbers into their logarithms, we can turn multiplication into addition. To work out 4 x 8, we see that log(4) = 2 (since 4 = 2 x 2), and that log(8) = 3 (since 8 = 2 x 2 x 2). We can then just do the addition: log(4) + log(8) = 2 + 3 = 5, and look that up in our inverse-log table to get 32.
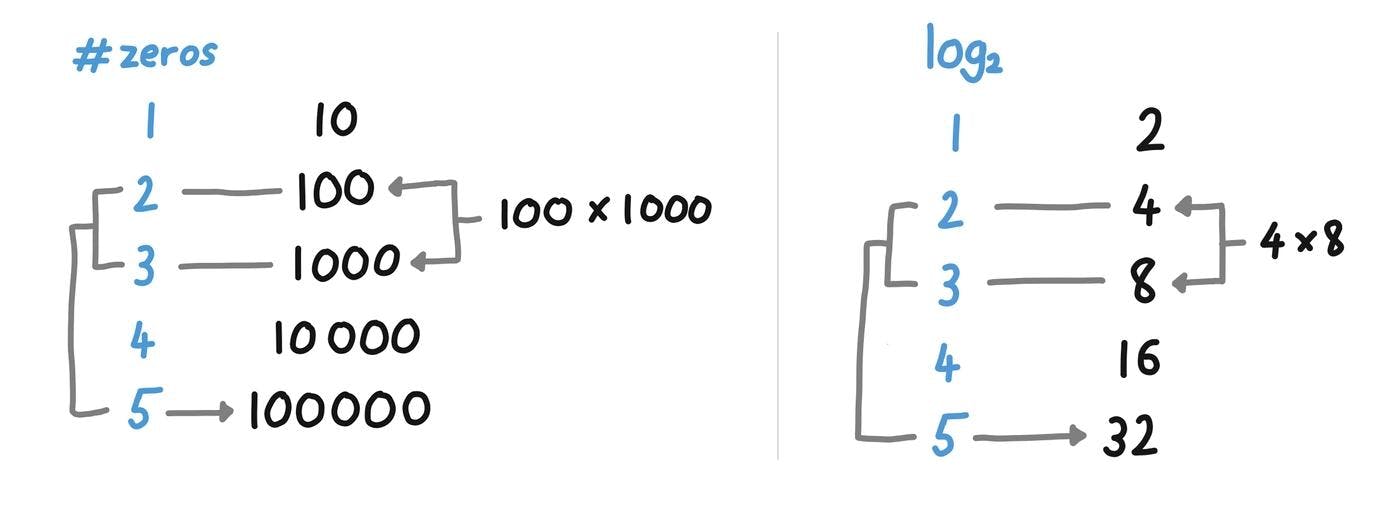
Formally, we’re using this identity to re-write multiplication into addition:
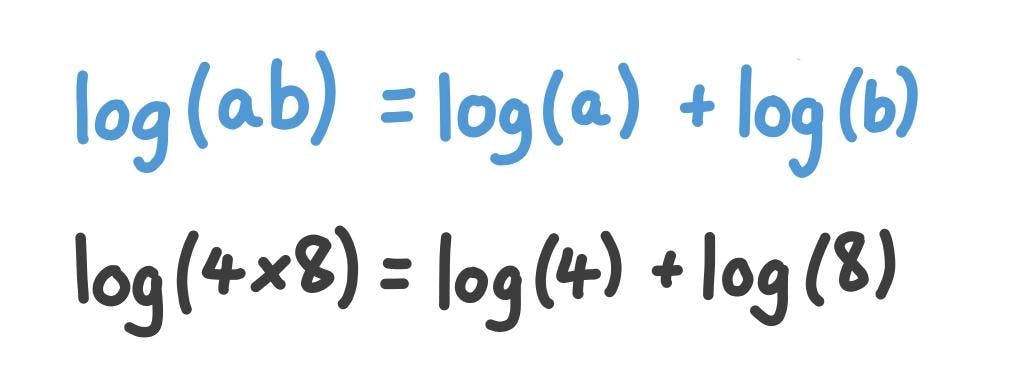
How does this relate to the slide-rule?
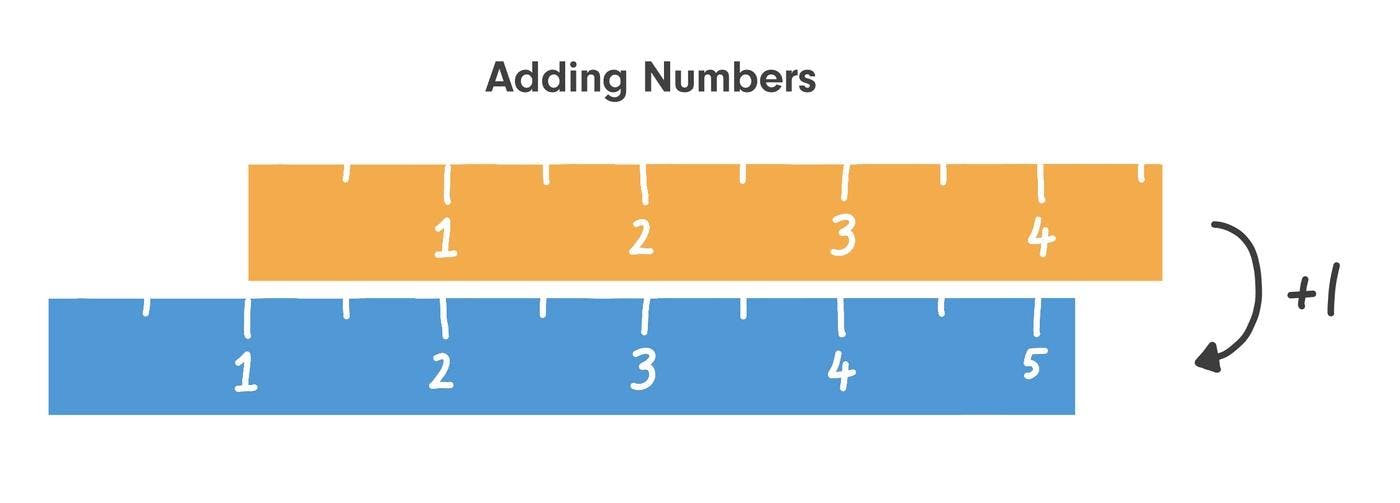
If we had two sticks with linear scales, we could use them to add numbers together. Suppose you slide the top stick by a distance of 1 unit. The bottom stick will now show the result of adding 1 to each number on the top stick.
If we had two sticks with logarithmic scales, we could use them to add logarithms together in the same way. But as we know, adding logarithms lets us multiply numbers!
Suppose you slide the top stick by a distance of log(2). The bottom stick will now show the result of multiplying by 2 each number on the top stick.
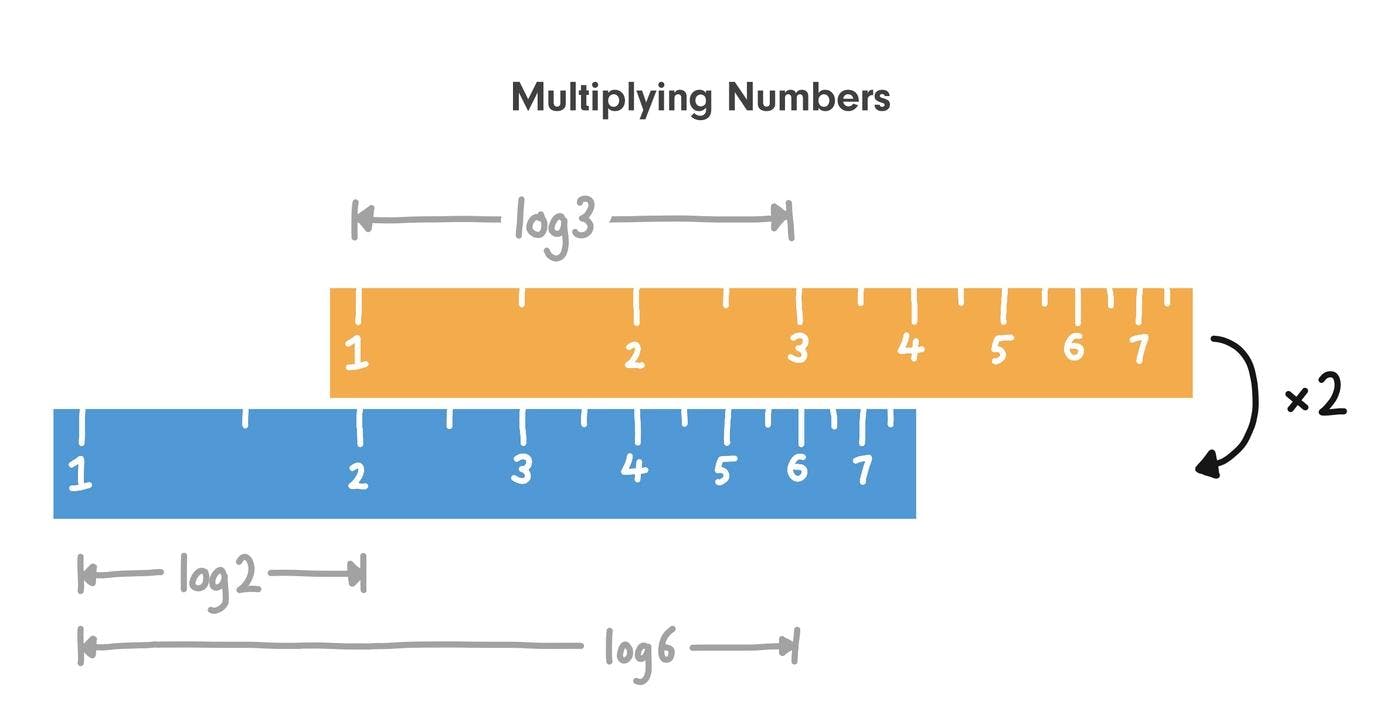
This is the slide rule v1.0 — two sliding sticks with logarithmic scales. Different calculations can be carried out by sliding the sticks by different amounts.
As time went on, the device gained more and more bells and whistles allowing it to do more and more things.
The first problem was multiplying bigger and bigger numbers. Doing this without making the slide rule longer required more and more precision on the scales, the equivalent of having millimeters and tenths-of-millimeters on a centimeter rule. A movable pointer called a "cursor" was developed to make it easier to read numbers off more precisely. (This is likely the origin of the computer cursor!)
Next, people wanted to do more than just multiplication. Different scales were developed for squares, square roots, trigonometric functions, their hyperbolic equivalents, and an array of niche functions corresponding to specific applications. The standard slide rule eventually had 6 different scales for different functions.
Soon, people started framing problems so they’d be easy to solve on slide-rules. And they even devised algorithms to solve more complex problems, like calculating arbitrary powers, composing different functions, and solving quadratic equations.
The slide rule is an elegant piece of mathematics represented in an equally elegant physical representation. In spite of its simplicity, the slide rule is all around us — it's designed major structures in modern history, and taken us to the moon.
The last slide rule manufactured in the US was produced on July 11, 1976, marking 354 years of service. Not a bad run!




